آشنایی با چندوجهیها/بریدن کامل
بريدن كامل فرآيندى است كه در آن وسط اضلاع چندوجهى را مشخص و سپس رئوسش را تا آن نقاط مى برند. چندوجهى حاصل داراى وجوه شکل گوشه ها و وجوه كامل بريده چندوجهى اوليه است.
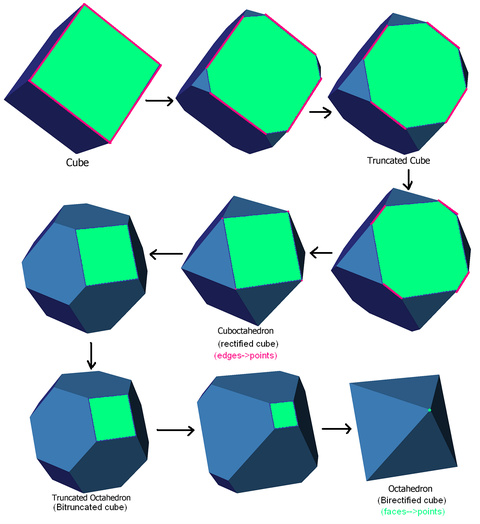
دو كامل بريدن عملى است كه در آن وجوه چندوجهى به يك رأس كاهش مى يابد. شكل زير عمل دو كامل بريدن را روى مكعب نشان مى دهد. شكل بالاچپ مكعب، شكل ميانى كامل بريده مكعب (مكعب هشت وجهى) و شكل پايانى دو كامل بريده مكعب (هشت وجهى) است. عكس اين قضيه روى هشت وجهى نيز واقف است:
در چندوجهى ها چندوجهى حاصل از دو كامل بريدن چندوجهى دوگانش است.
اجسام افلاطونى
ویرایشهر جسم افلاطونى (چندوجهى محدب منتظم) و دوگان آن چندوجهی كامل بريده یکسانی دارند. (این در مورد پلیتوپ ها در ابعاد بالاتر درست نیست.):
چندوجهی كامل بريده شده جسمى افلاطونی با كامل بريده دوگانش برابر است. به همین دلیل، نام آن ترکیبی از نام چندوجهى اصلی و دوگانش است است:
- بريده كامل چهاروجهى، که دوگان آن چهاروجهى است ، چهارچهاروجهى است که با نام هشت وجهى شناخته می شود.
- بريده كامل هشت وجهى، که دوگان آن مکعب است ، مکعب هشت وجهى است.
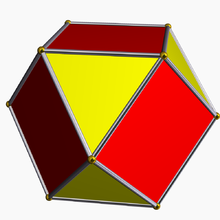
- كامل بريده بيست وجهى، که دوگان آن دوازده وجهى است ، بيست دوازده وجهى است.
اين موضوع در جدول زير بهتر مشاهده مى شود:
| چندوجهى اصلى | كامل بريده | دوگان |
|---|---|---|
| چهاروجهى منتظم |
چهارچهاروجهى (هشت وجهى) |
چهاروجهى منتظم |
| مكعب |
مكعب هشت وجهى |
هشت وجهى منتظم |
| دوازده وجهى منتظم |
بيست دوازده وجهى |
بيست وجهى منتظم |
منابع
ویرایش- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, شابک ۰−۴۸۶−۶۱۴۸۰−۸ (pp. 145–154 Chapter 8: Truncation)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, شابک ۹۷۸−۱−۵۶۸۸۱−۲۲۰−۵ (Chapter 26)