هر گاه بین سطح و سیال مجاور اختلاف درجه حرارت وجود داشته باشد انتقال حرارت جابجایی اتفاق می‌افتد، مانند شکل زیر، یعنی زمانی که یک سیال از روی سطح عبور می‌کند.

مقدمه

{\frac {dQ}{dt}}=h\cdot A(T_{\text{env}}-T_{0})

انرژی گرمایی : $Q=$ Thermal energy in Joules

ضریب انتقال حرارت : $h=$ Heat transfer coefficient

سطح موثر : $A=$ Surface area of the heat being transferred

دمای سطح جسم: $T_{0}=$ Temperature of the object's surface

دمای محیط: $T_{\text{env}}=$ Temperature of the environment

در قانون سرمایش نیوتن h به عوامل زیر بستگی دارد:

۱- جنس سیال یعنی هوا باشد یا آب باشد

۲- نحوه قرار گرفتن جسم (عمودی یا افقی و یا مورب)

۳- h سیال در جوشش خیلی زیاد است

۴- به شکل جسم بستگی دارد (کروی، تخت یا استوانه‌ای)

مکانیزم جابجایی آزاد

در جابجایی آزاد هیچ عامل خارجی وجود ندارد و حرکت سیال فقط در اثر تاثیر دانسیته می‌باشد مانند حرکت هوا از روی سطح شوفاژ. مثال برای جابجایی اجباری زمانی است مانند حرکت آب از داخل یک لوله با استفاده از یک پمپ در جابجایی آزاد سرعت سیال بسیار کم می‌باشد. بنابراین باتوجه به رابطه زیر مقدار انتقال حرارت بسیار کم می‌باشد.

جابجایی آزاد مکانیزم یا نوعی از انتقال حرارت می‌باشد که در آن حرکت سیال توسط یک منبع خارجی مثل پمپ و یا فن و دستگاه‌های مکش تامین نمی‌گردد اما فقط توسط اختلاف چگالی در سیال که توسط گرادیان دما تامین می‌شود انتقال میابد.

در جابجایی آزاد سیال منبع گرم را احاطه کرده و گرما دریافت می‌کند. و بدین سان چگالیش پایین میاید و سیال سرد جای آن را می‌گیرد و گرم می‌شود و بدین سان این چرخه ادامه پیدا می‌کند. این پروسه انرژی حرارتی را از سلول پایینی به بالا هدایت می‌کند.

نیروی راننده برای جابجایی آزاد نیروی بوینسی یعنی اختلاف چگالی بین دو سیال می‌باشد.

جابجایی آزاد در سالهای اخیر مورد توجه محققان قرار گرفته است و این توجه به دلیل وجود این نوع جابجایی در طبیعت و نیز کاربردهای آن در مهندسی می‌باشد. در طبیعت سلول‌های جابجایی از طلوع آفتاب و نور خورشید زمین و آب را گرم کرده و این اصلی ترین صورت سیستم آب و هوایی می‌باشد. همچنین این انتقال در جریانات اقیانوسی و نیز در جریان هوای گرم روی آتش و همچنین شکل گیری بادهای اقیانوسی دیده می‌شود.

در محاسبات ریاضیاتی این نوع جابجایی وابستگی سیستم بسوی جابجایی طبیعی به عدد گراشف (Grashof Number) که نرخ نیروی بوینسی و نیروی ویسکوز می‌باشد.

$Gr={\frac {g\beta ({{T}_{S}}-{{T}_{\infty }}){{L}^{3}}}{{\nu }^{2}}}$

که در آن:

g: شتاب گرانش

T_s: دمای سطح

T: دمای هوای آزاد

L: طول مشخصه

ν: ویسکوزیته

β: ضریب انبساط برای مایعات که جدول‌بندی شده است، به علاوه می‌توانیم از فرمول زیر نیز استفاده کنیم:

\beta ={\frac {1}{V}}{\frac {dV}{dT}}={\frac {1}{v}}{\frac {dv}{dT}}=-{\frac {1}{\rho }}{\frac {d\rho }{dT}}

(K^-1)

برای گازهای ایده ال به راحتی این عدد را می‌توان یافت:

PV=nRT\,

PV={\frac {m}{mol.weight}}RT

{\frac {m}{V}}=\rho \ ={\frac {P\times mol.weight}{RT}}

{\frac {d\rho }{dT}}=-{\frac {P\times mol.weight}{R}}{\frac {1}{T^{2}}}

\beta =-{\frac {1}{\rho }}{\frac {d\rho }{dT}}=-\left({\frac {RT}{P\times mol.weight}}\right)\left(-{\frac {P\times mol.weight}{R}}{\frac {1}{T^{2}}}\right)={\frac {1}{T}}

β برای گازهای ایده‌آل طبق معادله حالت چنین بدست می‌آید:

\beta ={\frac {1}{T}}

$[\beta ]={\frac {1}{K}}$

یک فرمول ساده را برای جابجایی آزاد به موجب تمرکز گرادیان می‌توان نوشت:

$Gr={\frac {g\beta \left({{T}_{s}}-{{T}_{\infty }}\right){{L}^{3}}}{{\nu }^{2}}}$

(عدد گراشوف= $Gr$ )

حال اگر ${\frac {Gr}{Re^{2}}}\gg 1$ جابجایی اجباری قابل صرف نظر کردن است. در این حالت:

$N{{u}_{L}}=f\left({{\operatorname {Re} }_{L}},\Pr \right)$

اگر ${\frac {Gr}{Re^{2}}}\ll 1$ جابجایی آزاد قابل صرف نظر می‌باشد. در این حالت:

$N{{u}_{L}}=f\left({{\operatorname {Re} }_{L}},\Pr \right)$

و اگر

${\frac {G{{r}_{L}}}{{\operatorname {Re} }_{L}}}\approx 1$ آثار ترکیبی جابجایی آزاد و جابجایی اجباری را باید در نظر گرفت. و در این حالت:

$N{{u}_{L}}=f\left({{\operatorname {Re} }_{L}},\Pr ,G{{r}_{L}}\right)$

جابجایی طبیعی به شدت به هندسه سطح گرم وابسته است و روابط گوناگونی برای محاسبه ضریب انتقال حرارت موجود است. عدد رایلی به کرات مورد استفاده می‌باشد:

$Ra=Gr.\Pr$ (Pr: عدد پرانتل)

{\textbf {Ra}}={\frac {\Delta \rho gL^{3}}{D\mu }}

که در آن:

$\Delta \rho$ اختلاف چگالی جزئی از ماده که مخلوط است، g شتاب گرانش، L طول مشخصه،

D مشخصه ساطع کننده، $\mu$ ویسکوزیته دینامیکی است.

یک رابطه عمومی که تنوع هندسه‌ها را اعمال می‌کند به صورت زیر است:

Nu=\left[Nu_{0}^{\frac {1}{2}}+Ra^{\frac {1}{6}}\left({\frac {f_{4}\left(Pr\right)}{300}}\right)^{\frac {1}{6}}\right]^{2}

که در آن f4 از رابطه زیر بدست میاید:

f_{4}(Pr)=\left[1+\left({\frac {0.5}{Pr}}\right)^{\frac {9}{16}}\right]^{\frac {-16}{9}}

NU عدد ناسلت می‌باشد و اندازه آن و مشخصه طول در جدول زیر آمده است:

Geometry	Characteristic Length	Nu₀
Inclined Plane	x (Distance along plane)	۰٫۶۸
Inclined Disk	9D/11 (D = Diameter)	۰٫۵۶
Vertical Cylinder	x (height of cylinder)	۰٫۶۸
Cone	4x/5 (x = distance along sloping surface)	۰٫۵۴
Horizontal Cylinder	$\pi D/2$ (D = Diameter of cylinder)	0.36 $\pi$

جابجایی آزاد روی صفحه عمودی

در این سیستم گرما از یک صفحه عمودی به سیال با حرکت موازی روی آن با جابجایی طبیعی انتقال می‌یابد. این مکانیزم در سیستمی که سیال در حال حرکت با موقعیت چگالیش تغییر می‌کند رخ می‌دهد. این پدیده هنگامی اهمیت پیدا می‌کند که نیروی اجباری به سیال وارد نشود.

در جابجایی آزاد چون دما عامل حرکت است، پس لایه مرزی سرعت و لایه مرزی گرمایی برهم منطبق اند.

شرایط مرزی:

${\begin{aligned}&y=0:u=v=0,T={{T}_{s}}\\&y\to \infty :u\to 0,T\to {{T}_{\infty }}\\\end{aligned}}$

فرضیات لایه مرزی:

${\begin{aligned}&{\frac {d{{p}_{\infty }}}{dx}}=-{{\rho }_{\infty }}g\\&\delta <<L\to u>>\nu ,{\frac {\partial }{\partial x}}<<{\frac {\partial }{\partial y}}\\\end{aligned}}$

معادلات ناویر استوکس و پیوستگی را در راستای x و y برای شرایط دایمی می‌نویسیم:

${\begin{aligned}&{\frac {\partial u}{\partial x}}+{\frac {\partial \nu }{\partial y}}=0\\&{{\rho }_{\infty }}(u{\frac {\partial u}{\partial x}}+\nu {\frac {\partial u}{\partial y}})=-{\frac {\partial P}{\partial x}}+{{\rho }_{\infty }}(1-\beta (T-{{T}_{\infty }}))g+\mu {\frac {{{\partial }^{2}}u}{\partial {{x}^{2}}}}\\&{{\rho }_{\infty }}(u{\frac {\partial \nu }{\partial x}}+\nu {\frac {\partial \nu }{\partial y}})=-{\frac {\partial P}{\partial y}}+0+\mu {\frac {{{\partial }^{2}}\nu }{\partial {{y}^{2}}}}\Rightarrow {\frac {\partial P}{\partial y}}=0\Rightarrow P(x,y)={{P}_{\infty }}(x)\\&{\frac {\partial P}{\partial x}}={\frac {dP}{dx}}={\frac {d{{P}_{\infty }}}{dx}}=-{{\rho }_{\infty }}g\\\end{aligned}}$

معادله تکانه خطی x:

${\begin{aligned}&\to {{\rho }_{\infty }}(u{\frac {\partial u}{\partial x}}+\nu {\frac {\partial u}{\partial y}})={{\rho }_{\infty }}g-{{\rho }_{\infty }}(1-\beta (T-{{T}_{\infty }}))g+\mu {\frac {{{\partial }^{2}}u}{\partial {{y}^{2}}}}={{\rho }_{\infty }}\beta (T-{{T}_{\infty }})g+\mu {\frac {{{\partial }^{2}}u}{\partial {{y}^{2}}}}\\&{{\rho }_{\infty }}{{C}_{p}}(u{\frac {\partial T}{\partial x}}+\nu {\frac {\partial T}{\partial y}})=k{\frac {{{\partial }^{2}}T}{\partial {{y}^{2}}}}\\\end{aligned}}$

${\begin{aligned}&{{x}^{*}}={\frac {x}{L}},{{y}^{*}}={\frac {y}{L}},{{u}^{*}}={\frac {u}{{u}_{0}}},{{\nu }^{*}}={\frac {\nu }{{u}_{0}}},{{T}^{*}}={\frac {T-{{T}_{\infty }}}{{{T}_{s}}-{{T}_{\infty }}}}\\&{\frac {{u}_{0}}{L}}{\frac {\partial {{u}^{*}}}{\partial {{x}^{*}}}}+{\frac {{u}_{0}}{L}}{\frac {\partial {{\nu }^{*}}}{\partial {{x}^{*}}}}=0\to {\frac {\partial {{u}^{*}}}{\partial {{x}^{*}}}}+{\frac {\partial {{\nu }^{*}}}{\partial {{x}^{*}}}}=0\\&{\frac {{{u}_{0}}^{2}}{L}}{{u}^{*}}{\frac {\partial {{u}^{*}}}{\partial {{x}^{*}}}}+{\frac {{{u}_{0}}^{2}}{L}}{{\nu }^{*}}{\frac {\partial {{\nu }^{*}}}{\partial {{y}^{*}}}}=\beta {{T}^{*}}({{T}_{s}}-{{T}_{\infty }})g+\upsilon {\frac {{u}_{0}}{{L}^{2}}}{\frac {{{\partial }^{2}}{{u}^{*}}}{\partial {{y}^{*}}^{2}}}\\&\to {{u}^{*}}{\frac {\partial {{u}^{*}}}{\partial {{x}^{*}}}}+{{\nu }^{*}}{\frac {\partial {{\nu }^{*}}}{\partial {{y}^{*}}}}={\frac {L}{{{u}_{0}}^{2}}}\beta {{T}^{*}}({{T}_{s}}-{{T}_{\infty }})g+{\frac {\upsilon }{{{u}_{0}}L}}{\frac {{{\partial }^{2}}{{u}^{*}}}{\partial {{y}^{*}}^{2}}}\\&{\frac {{u}_{0}}{L}}{{u}^{*}}({{T}_{s}}-{{T}_{\infty }}){\frac {\partial {{T}^{*}}}{\partial {{x}^{*}}}}+{\frac {{u}_{0}}{L}}{{\nu }^{*}}({{T}_{s}}-{{T}_{\infty }}){\frac {\partial {{T}^{*}}}{\partial {{y}^{*}}}}=\alpha {\frac {{{T}_{s}}-{{T}_{\infty }}}{{L}^{2}}}{\frac {{{\partial }^{2}}{{T}^{*}}}{\partial {{y}^{*}}^{2}}}\\&{{u}^{*}}{\frac {\partial {{T}^{*}}}{\partial {{x}^{*}}}}+{{\nu }^{*}}{\frac {\partial {{T}^{*}}}{\partial {{y}^{*}}}}={\frac {\upsilon \alpha }{\nu {{u}_{0}}L}}{\frac {{{\partial }^{2}}{{T}^{*}}}{\partial {{y}^{*}}^{2}}}\\&{\frac {\beta g({{T}_{s}}-{{T}_{\infty }})L}{{{u}_{0}}^{2}}}=1\to {{u}_{0}}={\sqrt {\beta g({{T}_{s}}-{{T}_{\infty }})L}}\\&{{\operatorname {Re} }^{2}}={\frac {{{u}_{0}}^{2}{{L}^{2}}}{{\upsilon }^{2}}}={\frac {\beta g({{T}_{s}}-{{T}_{\infty }}){{L}^{3}}}{{\upsilon }^{2}}}=G{{r}_{L}}\\&{{u}^{*}}{\frac {\partial {{u}^{*}}}{\partial {{x}^{*}}}}+{{\nu }^{*}}{\frac {\partial {{u}^{*}}}{\partial {{y}^{*}}}}={{T}^{*}}+{\frac {1}{\sqrt {G{{r}_{L}}}}}{\frac {{{\partial }^{2}}{{u}^{*}}}{\partial {{x}^{*}}^{2}}}\\&{{u}^{*}}{\frac {\partial {{T}^{*}}}{\partial {{x}^{*}}}}+{{\nu }^{*}}{\frac {\partial {{T}^{*}}}{\partial {{y}^{*}}}}={\frac {1}{{\sqrt {G{{r}_{L}}}}\Pr }}{\frac {{{\partial }^{2}}{{T}^{*}}}{\partial {{y}^{*}}^{2}}}\\&Nu=f(Gr,\Pr )\\&Gr*\Pr =Ra,Ra={\frac {\beta g({{T}_{s}}-{{T}_{\infty }}){{L}^{3}}}{\alpha \upsilon }}\\\end{aligned}}$

${\begin{aligned}&{{10}^{4}}<Ra<{{10}^{9}}:{\overline {N{{u}_{L}}}}=.5R{{a}_{L}}^{\frac {1}{4}}\\&{{10}^{9}}<Ra<{{10}^{13}}:{\overline {N{{u}_{L}}}}=.1R{{a}_{L}}^{\frac {1}{3}}\\\end{aligned}}$

هم برای آشفته و هم برای لایه‌ای برقرار است:

${\overline {N{{u}_{L}}}}={{(.825+{\frac {.387R{{a}^{\frac {1}{6}}}}{{[1+{{({\frac {.492}{\Pr }})}^{\frac {9}{16}}}]}^{\frac {8}{27}}}})}^{2}}$

${{T}_{\infty }}$ : دمای سیال مجاور

${{\rho }_{\infty }}$ : چگالی سیال مجاور

${{T}_{s}}$ : دمای سطح

$\delta$ : ضخامت لایه مرزی

$u$ : مؤلفه سرعت در راستای x

$\nu$ : مؤلفه سرعت در راستای y

$\upsilon$ : لزجت سینماتیکی

${{x}^{*}}$ : متغیر بی بعد شده x

${{y}^{*}}$ : متغیر بی بعد شده y

${{T}^{*}}$ : بی بعد شده دما

${{u}^{*}}$ : بی بعد شده u

${{\nu }^{*}}$ : بی بعد شده v

$\operatorname {Re}$ : عدد بی بعد رینولدز

$\Pr$ : عدد بی بعد پرانتل

$Ra$ : عدد بی بعد رایلی

$Gr$ : عدد بی بعد گراشف

$Nu$ : عدد بی بعد ناسلت

${\overline {N{{u}_{L}}}}$ : ناسلت میانگین

هنگامی که جریان سیال را به واسطه گرمادهی در نظر بگیریم روابط زیر قابل استفاده می‌باشد با فرض ایده‌آل و دو اتمی بودن سیال و صفحه در دمای ثابت و جریان سیال کاملا آرام:

Nu_m = 0.478(Gr^0.25)

Mean Nusselt Number = Nu_m = h_mL/kمیانگین عدد ناسلت

Where

h_m = mean coefficient applicable between the lower edge of the plate and anyمیانگین ضریب انتقال حرارت point in a distance L (W/m². °K)

L = height of the vertical surface (m) ارتفاع عمودی

k = thermal conductivity (W/m. °K) رسانندگی گرمایی

عدد گراشف Grashof Number = Gr = [gL³(t_s-t∞)]/v²T

Where

g = gravitational acceleration (m/s²) شتاب گرانش

L = distance above the lower edge (m) فاصله از لبه پایینی

t_s = temperature of the wall (°K) دمای دیواره

t∞ = fluid temperature outside the thermal boundary layer (°K) دمای سیال بیرون

v = velocity of the fluid (m/s) سرعت سیال T = absolute temperature (°K) دمای مطلق

هنگامی که جریان آشفته می‌باشد می‌بایست از روابط مربوط به خود استفاده گردد.

مثالی از جابجایی آزاد روی صفحه قائم

مقدار انتقال حرارت را بدست آورید.

ابتدا خواص را از جدول می‌خوانیم و با استفاده از آنها رایلی را بدست می‌آوریم.

با رایلی بدست آمده ناسلت میانگین را محاسبه می‌کنیم و از این طریق ضریب انتقال حرارت جایجایی بدست می‌آید.

با داشتن ضریب انتقال حرارت جایجایی، حرارت مبادله شده قابل محاسبه است.

${\begin{aligned}&Ra={\frac {\beta g({{T}_{s}}-{{T}_{\infty }}){{L}^{3}}}{\alpha \upsilon }}\\&{{T}_{f}}={\frac {{{T}_{s}}+{{T}_{\infty }}}{2}}={{102.5}^{0}}F=562.5R\\&k=0.01535{\frac {Btu}{(hr)(ft){{(}^{0}}F)}}\\&\upsilon =0.1825*{{10}^{-3}}{\frac {f{{t}^{2}}}{s}}\\&\Pr =.726\\&\beta ={\frac {1}{{T}_{f}}}=0.00178{{R}^{-1}}\\&Ra=5.5*{{10}^{8}}\to La\min ar\\&{\overline {N{{u}_{L}}}}={{(.825+{\frac {.387R{{a}^{\frac {1}{6}}}}{{[1+{{({\frac {.492}{\Pr }})}^{\frac {9}{16}}}]}^{\frac {8}{27}}}})}^{2}}=102.6\\&{\overline {h}}={\frac {{\overline {N{{u}_{L}}}}k}{L}}=.787{\frac {Btu}{(hr)(f{{t}^{2}}){{(}^{0}}F)}}\\&q={\overline {h}}{{A}_{s}}({{T}_{s}}-{{T}_{\infty }})=173{\frac {Btu}{hr}}\\\end{aligned}}$

نمونه مسئله

۱) صفحه عمودی بزرگی با دمای یکنواخت ۱۳۰ درجه سانتی گرادرا که در هوای اتمسفریک ساکن ۲۵ درجه سانتی گرادو فشار ۱ اتمسفر آویزان است در نظر بگیرید.

الف) ضخامت لایه مرزی رادر فاصلهٔ ۰٫۲۵ متری از لبهٔ ابتدایی تخمین بزنید.

ب) سرعت ماکزیمم در لایه مرزی چقدر است؟

ج) با استفاده از حل تشابه‌ای ضریب انتقال گرما را در ۰٫۲۵ متری بیابید.

د) در چه مکانی روی صفحه از لبهٔ ابتدایی لایه مرزی متلاطم می‌شود؟

۲) شیشهٔ عمودی عقب اتومبیلی به ضخامت L=8mm و به ارتفاع H=0.5m استودارای گرمکن شبکه‌ای ظریفی، با گرمایش حجمی تقریباً یکنواخت (q(w/m³است.

الف) شرایط پایایی رادر نظر بگیرید، که در آن سطح داخلی شیشه در معرض هوای ساکن ۲۰ درجه سانتی گراد است وسطح خارجی در معرض هوای ۱۰- سانتی گراد، که با سرعت20m/s با جریان موازی روی سطح حرکت می‌کند، قرار دارد. مطلوب است آهنگ گرمایش حجمی لازم برای اینکه سطح داخلی شیشه در ۱۵ درجه سانتی گراد بماند.

۳) مطلوب است شار گرمایی یکنواخت ماکزیمم مجاز که می‌توان به یک پنل داد، به طوری که وقتی دمای هوای اطراف ۲۵ درجه سانتی‌گراد است ماکزیمم دمای پنل از ۳۷ درجه سانتی گراد بیشتر نشود.

۴)یک پنل گرمکن تخت و تک دما به عرض ۰٫۵ متر و ارتفاع ۱ متر به یکی از دیوارهای اتاق بزرگی نصب شده است. سطح پنل دارای گسیلمندی ۰٫۹ است ودر دمای ۴۰۰ کلوین است. اگر دیوارها وهوای اتاق در ۳۰۰ کلوین باشند، آهنگ خالص انتقال گرما از پانل به اتاق چقدر است؟

مثال حل شده

جریان هوای گرم در مجرای مستطیلی بلندی به عرض ۰٫۷۵ متر و به ارتفاع ۰٫۳ متر سطح خارجی مجرا را در ۴۵ درجه سانتی‌گراد نگه می‌دارد. اگر مجرا غیر عایق و در معرض هوای ۱۵ درجه سانتیگراد محوطه گربه رو خانه‌ای قرار داشته باشد دفع گرما از یک متر طول مجرا چقدر است؟

حل:

داده: دمای سطح مجرای مستطیلی.

خواسته: دفع گرما از یک متر طول مجرا.

طرحواره

فرض

هوای محیط ساکن است.
تشعشع در سطح ناچیز است.

خواص:

از جدول الف - ۴ برای هوا در دمای فیلم ۳۰۳ کلوین داریم:

$T_{f}=303k$

$k=0.0265{\frac {w}{m.k}}$

$pr=0.71$

$\nu =16.2*10^{-6}{\frac {m^{2}}{s}}$

$\alpha =22.9*10^{-6}{\frac {m}{s}}$

$\beta =0.0033{\frac {1}{k}}$

تحلیل:

دفع گرما در سطح با جابجایی آزاد از جوانب عمودی و سطوح افقی بالایی و پایینی روی می‌دهد از معادله زیر:

Ra_{L}={\frac {g\beta \Delta TL^{3}}{\nu \alpha }}

با جایگذاری مقادیر در رابطه بالا:

{Ra}_{L}={\frac {g\beta \Delta TL^{3}}{\nu \alpha }}=2.62*10^{9}L^{3}

برای دو طرف L=H=۰٫۳ از این رو: ${Ra}_{L}=7.07*10^{7}$ . لذا لایه مرزی جابجایی آزاد لایه‌ای است و از معادله زیر:

${\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.67\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{9}$

${\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.67\mathrm {(} 7.07*10^{7})^{1/4}}{\left[1+(0.492/\mathrm {0.71} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{9}$

${\overline {\mathrm {Nu} }}_{L}\ =47.887$

${\bar {h_{s}}}={\frac {k{\bar {Nu_{l}}}}{L}}=(0.0265)(47.88)/(0.3)=4.23{\frac {w}{m^{2}.k}}$

برای سطوح بالایی و پایینی L=0.375 m از این رو: ${Ra}_{L}=1.38*10^{8}$ و به ترتیب از معادله‌های زیر داریم :

${\overline {\mathrm {Nu} }}_{L}\ =0.15\mathrm {Ra} _{L}^{1/3}=77.4\,\quad 10^{7}\leq \mathrm {Ra} _{L}\leq 10^{11}$

${\bar {h_{t}}}={\frac {k{\bar {Nu_{l}}}}{w/2}}=(0.0265)(77.4)/(0.375)=5.47{\frac {w}{m^{2}.k}}$

${\overline {\mathrm {Nu} }}_{L}\ =0.27\mathrm {Ra} _{L}^{1/4}=29.29\,\quad 10^{5}\leq \mathrm {Ra} _{L}\leq 10^{10}$

${\bar {h_{b}}}={\frac {k{\bar {Nu_{l}}}}{w/2}}=(0.0265)(29.29)/(0.375)=2.07{\frac {w}{m^{2}.k}}$

آهنگ انتقال حرارت در طول مجرا:

$q={\bar {h}}\cdot A(T-T_{\infty })$
$=[2{\bar {h_{s}}}(L)+{\bar {h_{t}}}(w)+{\bar {h_{b}}}(w)](T-T_{\infty })$
$=(2*4.23*0.3+5.47*0.75+2.07*0.75)(45-15)=246{\frac {w}{m}}$

رابطه‌های تجربی برای جریان‌های جابجایی آزاد خارجی

دراینجا می‌خواهیم در مورد رابطه‌های تجربی که برای شکل‌های هندسی معمولی غوطه‌ور (جریان‌های خارجی) به دست آمده‌اند به طور خلاصه بحث کنیم.

ابتدا عدد ریلی را به صورت زیر تعریف می‌کنیم:

\mathrm {Ra} _{l}=\mathrm {Gr} _{l}\mathrm {Pr} ={\frac {g\beta }{\nu \alpha }}(T_{s}-T_{\infty })l^{3}

در این رابطه، $L$ ، طول مشخصه شکل تعریف می‌شود و همچنین باید دانست تمام خواص در دمای فیلم (که برابر است با یک دوم مجموع دمای سطح و دمای بینهایت) ارزیابی می‌شوند.

T_{f}={\frac {T_{s}+T_{\infty }}{2}}

اولین رابطه را برای صفحه عمودی بررسی می‌کنیم.

صفحات عمودی

چرچیل و چو رابطه‌ای داده‌اند که برای تمام گستره ریلی قابل استفاده و به صورت زیر است:

${\overline {\mathrm {Nu} }}_{L}\ ={\left[0.825+{\frac {0.387\mathrm {Ra} _{L}^{1/6}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{8/27}\,}}\right]}^{2}$

گرچه معادله فوق در اغلب محاسبات مهندسی مفید است ولی رابطه زیر برای جریان لایه‌ای دقت بالاتری دارد:

${\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.67\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{9}$

البته باید توجه داشت که دو رابطه بالا برای صفحات تک دما هستند. اگر به جای حالت تک دما، شار گرمای یکنواخت در سطح برقرار باشد، اختلاف دمای سطح و دمای بینهایت بر حسب $x$ تغییر و از مقدار صفر در لبه ابتدایی شروع به افزایش می‌کند.

نتایج فوق‌الذکر را برای استوانه‌های عمودی به طول $L$ می‌توان به کار برد به شرطی که ضخامت لایه مرزی خیلی کمتر از قطر استوانه باشد این شرط وقتی برقرار است که

${\frac {D}{L}}\rangle {\frac {35}{G.{{r}^{0.25}}}}$

سبسی و مینکوویچ و اسپارو نتایجی را برای استوانه‌های باریک و عمودی که شرط فوق را برآورده نمی‌کنند به دست آورده‌اند. در این استوانه‌ها، انحنای عرضی بر گسترش لایه مرزی تاثیر می‌گذارد و آهنگ انتقال گرما را افزایش می‌دهد.

مثال) در شکل مقابل مطلوبست :

${{\dot {Q}}_{conv}}$ ، ${{\dot {Q}}_{vap}}$ ، ${{\dot {Q}}_{rad}}$

توضیحات:
۱- چونکه شکل مساله یک استوانه عمودی است با توجه به نکته گفته شده در بالا ابتدا شرط ${\frac {D}{L}}\geq {\frac {35}{G{{r}^{\frac {1}{4}}}}}$ را بررسی می‌کنیم اگر صدق کرد آنگاه می‌توانیم از نتایج صفحه تخت برای صفحه عمودی استفاده کرد.(همانطور که در ادامه مشخص شده است این شرط برقرار است.)
۲-برای محاسبه ${{\dot {Q}}_{rad}},{{\dot {Q}}_{vap}}$ می‌توان با استفاده از فرمول‌هایی که در زیر گفته شده است استفاده کنیم.
۳-برای محاسبه ${{\dot {Q}}_{conv}}$ ابتدا باید با استفاده از جابجایی آزاد ${{\overline {Nu}}_{L}}$ و سپس ${{\overline {h}}_{L}}$ بدست آورده، آنگاه ${{\dot {Q}}_{conv}}={{\overline {h}}_{L}}A\left({{T}_{s}}-{{T}_{\infty }}\right)$ که در آن $A=\pi DL$

${\begin{aligned}&{{\dot {Q}}_{conv}}=hL\pi D({{T}_{s}}-{{T}_{\infty }})\\&{{\dot {Q}}_{rad}}=\varepsilon \sigma L\pi d({{T}_{s}}^{4}-{{T}_{surr}}^{4})=56.1w\\&{{\dot {Q}}_{vap}}={\dot {m}}{{h}_{fg}}\\&{{\dot {Q}}_{vap}}={{\dot {m}}_{v}}{{h}_{fg}}=2\left[{\frac {kg}{hr}}\right]*\left[{\frac {1hr}{3600s}}\right]*2257*{{10}^{6}}\left[{\frac {j}{kg}}\right]=1254w\\&{{T}_{f}}={\frac {{{T}_{s}}+{{T}_{\infty }}}{2}}=61.5{}^{\circ }c\\&k=0.028{\frac {w}{mk}}\\&\nu =1.9*{{10}^{-5}}{\frac {{m}^{2}}{s}}\\&Pr=0.72\\&\beta ={\frac {1}{T}}={\frac {1}{61.5+273.15}}=0.00299{{k}^{-1}}\\&G{{r}_{L}}={\frac {g\beta \left({{T}_{s}}-T\infty \right){{L}^{3}}}{{\nu }^{2}}}=1.1*{{10}^{5}}\\&{\frac {35L}{G{{r}^{\frac {1}{4}}}}}=0.07\prec D\\&R{{a}_{L}}=G{{r}_{L}}.\Pr =7.3*{{10}^{6}}\\&{{\overline {Nu}}_{L}}={{\left\{0.825+{\frac {0.387R{{a}_{L}}^{\frac {1}{6}}}{{\left[1+{{\left({\frac {0.492}{\Pr }}\right)}^{\frac {9}{16}}}\right]}^{\frac {8}{27}}}}\right\}}^{2}}=28.6\\&\Rightarrow {\overline {h}}={\frac {K}{L}}{\overline {Nu}}=6.7{\frac {w}{{{m}^{2}}k}}\\&\Rightarrow {{\dot {Q}}_{conv}}=46.2w\\\end{aligned}}$

ناسلت متوسط برای شرط مرزی شار ثابت در صفحه تخت قایم

${\overline {{N}_{{u}_{L}}}}={\frac {{\overline {h}}L}{K}}={\frac {{q}''L}{K({{T}_{\frac {L}{2}}}-T\infty )}}$

صفحات مایل و افقی

در صفحات عمودی، که از سیال محیط گرمتر (یا سردتر) هستند، صفحه در امتداد بردار گرانشی است، ونیروی شناوری تنها نیرویی است که باعث حرکت سیال در امتداد عمودی رو به بالا (یا رو به پایین) می‌شود. ولی اگر صفحه نسبت به گرانش مایل باشد، نیروی شناوری در امتداد عمود برسطح صفحه، و همچنین در امتداد موازی با آن، مولفه دارد. با کاهش مولفه نیروی شناوری موازی با سطح، سرعت سیال در امتداد صفحه کاهش می‌یابد، وانتفال گرمای جابجایی کم می‌شود. در حقیقت، وجود این کاهش بستگی دارد به این که انتفال گرما از سطح بالایی صفحه مورد توجه است یا از سطح پایینی آن.

اگر صفحه سرد باشد، مولفه $Y$ نیروی شناوری، که عمود بر صفحه است، جریان سقوطی لایه مرزی را که با سطح بالایی صفحه تماس دارد حفظ می‌کند. چون مولفه $X$ شتاب گرانشی تا $g\times \cos(\theta )$ کاهش یافته است سرعت سیال در امتداد صفحه کاهش می‌یابد و ضریب انتقال گرما در سطح بالایی کم می‌شود.

ولی در سطح پایینی مولفه $Y$ نیروی شناوری باعث جدایی سیال از سطح می‌شود و، با خروج توده‌های سیال سرد از سطح، گسترش لایه مرزی متوقف می‌شود.

جریان حاصل سه بعدی است و سیال سردی که از سطح پایینی جدا می‌شود دائما توسط سیال گرمتر محیط جایگزین می‌شود. جایگزینی سیال سرد لایه مرزی توسط محیط گرمتر و کاهش ضخامت لایه مرزی گرمایی ناشی از آن، باعث افزایش انتقال گرمای جابجایی در سطح پایینی می‌شود.

در حقیقت، افزایش انتقال گرمای ناشی از جریان سه بعدی عموما بیشتر است از مقدار کاهش انتقال گرمایی که از کاهش مولفه $X$ شتاب گرانشی ناشی می‌شود، و در نتیجه، انتقال گرما به سطح پایینی افزایش می‌یابد.

ریچ در مطالعات اولیه انتقال گرما در صفحات مایل اظهار داشت ضرایب جابجایی را از رابطه‌های صفحه عمودی می‌توان تعیین کرد به شرطی که در محاسبه عدد ریلی به جای g از $g\times \cos(\theta )$ استفاده شود.

ولی پس ازآن معلوم شد که این روش فقط برای سطح بالایی صفحه سرد و سطح پایینی صفحه گرم قابل قبول است، و برای سطح بالایی صفحه گرم و سطح پایینی صفحه سرد مناسب نیست، زیرا دراین صفحات سه بعدی بودن جریان سبب محدودیت کاربرد رابطه‌های کلی می‌شود.

اگر صفحه افقی باشد، نیروی شناوری بر سطح عمود است. مانند صفحه مایل، نقش‌های جریان و انتقال گرما شدیدا بستگی دارند به اینکه سطح گرم باشد یا سرد، رو به بالا باشد یا رو به پایین. برای سطح سرد رو به بالا، صفحه مانع حرکت سیال به طرف پایین، و برای سطح گرم رو به پایین مانع حرکت سیال رو به بالا می‌شود. در نتیجه، جریان قبل از اینکه بتواند از لبه‌های صفحه صعود یا سقوط کند باید به طور افقی حرکت کند وانتقال گرمای جابجایی کمی کاهش می‌یابد.

برعکس در سطح سرد رو به پایین جریان بر اثر سقوط توده‌های سیال، و در سطح گرم رو به بالا، جریان بر اثر صعود توده‌های سیال به وجود می‌آید.

طبق پایستاری جرم، سیال سردی که در سطح سقوط می‌کند با سیال گرمتری که در محیط صعود می‌کند جایگزین می‌شود و سیال گرمی که از سطح صعود می‌کند با سیال سردتری که در محیط سقوط می‌کند جایگزین می‌شود و انتقال گرما به خوبی صورت می‌گیرد.

رابطه‌ها

سطح بالایی صفحه گرم یا سطح پایینی صفحه سرد:

${\overline {\mathrm {Nu} }}_{L}\ =0.54\mathrm {Ra} _{L}^{1/4}\,\quad 10^{4}\leq \mathrm {Ra} _{L}\leq 10^{7}$

${\overline {\mathrm {Nu} }}_{L}\ =0.15\mathrm {Ra} _{L}^{1/3}\,\quad 10^{7}\leq \mathrm {Ra} _{L}\leq 10^{11}$

سطح پایینی صفحه گرم یا سطح بالایی صفحه سرد:

${\overline {\mathrm {Nu} }}_{L}\ =0.27\mathrm {Ra} _{L}^{1/4}\,\quad 10^{5}\leq \mathrm {Ra} _{L}\leq 10^{10}$

همچنین باید به یاد داشت که طول مشخصه عبارتست از:

$L={\frac {{A}_{s}}{P}}$

که در آن A و P به ترتیب مساحت و محیط صفحه‌اند.

مثال

رسانندگی گرمایی و گسیلمندی سطح جسمی را بدست اورید که بین دو دمای نشان داده شده در شکل است و از پایین گرم می‌شود و از بالا در تماس با هوای ساکن است. قدرت ورودی در سطح پایین ۷۰وات بگیرید.(شرایط را پایا بگیرید)

درابتدا توضیحی مختصر در مورد مسئله می‌دهیم:

از پایین توسط مولدی مقداری گرما تولید می‌شود که به سطح پایینی می‌رسد حال این گرما از صفحه بوسیلهٔ هدایت به سطح ازاد در تماس با هوا می‌رسد. حال این گرما باید بوسیلهٔ جابجایی و تشعشع دفع شود تا شرایط پایا برقرار شود.

تمام خواص مربوط به هوا رادردمای فیلم در جدول الف-۴ کتاب اینکروپرامی خوانیم.

${\begin{aligned}&{{T}_{f}}=335.5k\\&\upsilon =19.5\times {{10}^{-6}}{{m}^{2}}/{s}\;\\&k=0.0289{w}/{m.k}\;\\&\alpha =27.8\times {{10}^{-6}}{{m}^{2}}/{s}\;\\&pr=0.273\\&\beta =0.00298{{k}^{-1}}\\\end{aligned}}$

بقای انرژی را برای صفحه می‌نویسیم دقت کنیم که منظور از q کل گرمای ورودی به سطح بالا است که باید همین مقدار گرما بوسیلهٔ جابجایی ازاد و تشعشع به محیط داده شود تا شرایط پایا بوجود اید.

$q={{p}_{elec}}$

با استفاده از معادله رسانش نیوتن ضریب رسانندگی را می‌یابیم. منظور از ترمی که در صورت است مقدار شاری است که به سطح پایینی وارد می‌شود وسپس بایدبوسیلهٔ رسانش به سطح بالایی برسند.

$k={\frac {\frac {{p}_{elec}}{{w}^{2}}}{{({{T}_{1}}-{{T}_{2}})}/{L}\;}}={\frac {{70w}/{{(0.25m)}^{2}}\;}{{50{}^{\circ }c}/{0.025m}\;}}=0.560{w}/{m.k}\;$

رابطه زیر جهت رسیدن به ضریب تشعشع پیموده شده‌اند که با گرفتن سطح بالایی که با هوای ازاد در تماس است به عنوان یک حجم کنترل بدست می اید.

${\begin{aligned}&{{p}_{elec}}={{q}_{conv}}+{{q}_{rad}}=\left[{\overline {h}}({{T}_{2}}-{{T}_{\infty }})+\varepsilon \sigma \left(T_{2}^{4}-T_{sur}^{4}\right)\right]{{w}^{2}}\\&\varepsilon ={\frac {\left({{p}_{elec}}/{{w}^{2}}\;\right)-{\overline {h}}({{T}_{2}}-{{T}_{\infty }})}{\sigma \left(T_{2}^{4}-T_{sur}^{4}\right)}}\\\end{aligned}}$

برای یافتن ضریب تشعشع باید ضریب انتقال گرمای جابجایی را داشته باشیم که برای محاسبهٔ ان نیز باید عدد بدون بعد رایلی را به دست آوریم اما قبل از ان باید L را بدست آوریم

${\begin{aligned}&L={{A}_{S}}/{P}\;={{W}^{2}}/{4W}\;={W}/{4}\;=0.0625m\\&R{{a}_{L}}=g\beta \left({{T}_{2}}-{{T}_{\infty }}\right){{L}^{3}}/{\upsilon \alpha }\;=9.86\times {{10}^{5}}\\\end{aligned}}$

حال می‌توانیم از معادلهٔ ۳۰-۹ کتاب اینکروپرا استفاده کنیم و ضریب جابجایی را بدست اوریم

${\overline {h}}={\frac {{\overline {N{{u}_{L}}}}K}{L}}={\frac {K}{L}}0.54Ra_{L}^{{1}/{4}\;}={\frac {0.0289{W}/{m.k}\;}{0.0625m}}0.54{{\left(9.86\times {{10}^{5}}\right)}^{{1}/{4}\;}}=7.87{w}/{{{m}^{2}}.k}\;$

حال که ضریب جابجایی ازاد بدست امد می‌توانیم ضریب تشعشع را می‌یابیم.

$\varepsilon ={\frac {{70w}/{{{\left(0.250\right)}^{2}}-7.87{w}/{{{m}^{2}}k\left({{75}^{{}^{\circ }}}c\right)}\;}\;}{5.67\times {{10}^{-8}}{w}/{{{m}^{2}}{{k}^{4}}}\;\left({{373}^{4}}-{{298}^{4}}\right){{k}^{4}}}}=0.815$

یک مثال عددی - حل بوسیله نرم‌افزار EES

- مطلوب است مقدار شار انتقال گرما عبوری از شیشه به ابعاد ۱٫۲ ×۲.

${\begin{aligned}&{{h}_{Conv}}={\frac {Nu.k}{L}}\\&{{h}_{rad}}=\sigma A({{T}_{in}}^{2}+{{T}_{S.in}}^{2})({{T}_{in}}+{{T}_{S.in}})\\&{{R}_{Conv.in}}={\frac {1}{{{h}_{Conv.in}}.A}}(eq.1)\\&{{R}_{Conv.out}}={\frac {1}{{{h}_{Conv.Out}}.A}}(eq.2)\\&{{R}_{Cond.}}={\frac {L}{K.A}}(eq.3)\\&{{R}_{Rad.in}}={\frac {1}{{{h}_{Rad}}.A}}(eq.4)\\&Q={\frac {{{T}_{in}}-{{T}_{S.in}}}{{{R}_{Conv.in}}+{{R}_{Rad.in}}}}(eq.5)\\&Q={\frac {{{T}_{S.out}}-{{T}_{Out}}}{{R}_{Conv.Out}}}(eq.6)\\&{{Q}_{=}}{\frac {{{T}_{S.in}}-{{T}_{S.Out}}}{{R}_{Cond.}}}(eq.7)\\\end{aligned}}$

${\overline {\mathrm {Nu} }}_{L}\ ={\left[0.825+{\frac {0.387\mathrm {Ra} _{L}^{1/6}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{8/27}\,}}\right]}^{2}(eq.8)$

${\begin{aligned}&Guess{\overset {}{\mathop {} }}\,{{T}_{S.in}}:\\&{{T}_{S.in}}{\xrightarrow {eq.1\And eq.4\And eq.8}}{{R}_{Conv.in}}\And {{R}_{Rad.in}}{\xrightarrow {eq.5}}{{Q}_{}}\\&{\xrightarrow {eq.3\And eq.7}}{{T}_{S.out}}{\xrightarrow {eq.8\And eq.2}}{{R}_{Conv.out}}{\xrightarrow {eq.6}}{{T}_{S.in}}\\\end{aligned}}$

حل بوسیله نرم‌افزارEES:

${\begin{aligned}&A=2.4[{{m}^{2}}]\mathop {,} _{}B=0.003431\mathop {,} _{}e=0.9\mathop {,} _{}{{h}_{1}}=2.913\mathop {,} _{}\\&{{h}_{2}}=7.678K=1.4[w/m-K]K\mathop {,} _{}{{f}_{1}}=0.04365K\mathop {,} _{}\\&{{f}_{2}}=0.04263L=1.2[m]Mi{{o}_{1}}=0.00002905\mathop {,} _{}\\&Mi{{o}_{2}}=0.00002848\mathop {,} _{}N{{u}_{1}}=80.09\mathop {,} _{}N{{u}_{2}}=216.1\mathop {,} _{}\\&P{{r}_{1}}=0.6936\mathop {,} _{}P{{r}_{2}}=0.6938\mathop {,} _{}{{p}_{1}}=101[kpa]\mathop {,} _{}{{Q}_{1}}=256.8[J]\\&{\text{Q}}\_{\text{1}}={\text{256}}.{\text{8 }}\left[{\text{J}}\right]\mathop {,} _{}{\text{Q}}\_{\text{2}}={\text{256}}.{\text{8 }}\left[{\text{J}}\right]~\mathop {,} _{}{\text{Q}}\_{\text{3}}={\text{256}}.{\text{8 }}\left[{\text{J}}\right]~\mathop {,} _{}\\&~~{\text{Ra}}={\text{2}}.{\text{493E}}+0{\text{8}}~\mathop {,} _{}~{\text{Re}}={\text{1352}}00\mathop {,} _{}{\text{Ro}}\_{\text{1}}=0.{\text{6233}}~~\mathop {,} _{}\\&{\text{Ro}}\_{\text{2}}=0.{\text{6418}}~~\mathop {,} _{}{\text{R}}\_{\text{1}}=0.{\text{143}}~\mathop {,} _{}~{\text{R}}\_{\text{2}}=0.0{\text{8243}}~~\mathop {,} _{}{\text{R}}\_{\text{3}}=0.0{\text{1}}0{\text{29}}\\&{\text{R}}\_{\text{4}}=0.0{\text{5427}}~~~\mathop {,} _{}{\text{Tf}}\_{\text{1}}={\text{291}}.{\text{4 }}\left[{\text{K}}\right]~~~\mathop {,} _{}{\text{Tf}}\_{\text{2}}={\text{275}}.{\text{1 }}\left[{\text{K}}\right]~~\mathop {,} _{}\\&~{\text{tic}}=0.00{\text{6 }}\left[{\text{m}}\right]~~\mathop {,} _{}{\text{T}}\_{\text{1}}={\text{298}}.{\text{2 }}\left[{\text{K}}\right]~~\mathop {,} _{}{\text{T}}\_{\text{2}}={\text{284}}.{\text{7 }}\left[{\text{K}}\right]~\mathop {,} _{}\\&{\text{T}}\_{\text{3}}={\text{282}}.{\text{1 }}\left[{\text{K}}\right]~~\mathop {,} _{}{\text{T}}\_{\text{4}}={\text{268}}.{\text{2 }}\left[{\text{K}}\right]~~~\mathop {,} _{}{\text{Vel}}={\text{5 }}\left[{\text{m}}/{\text{s}}\right]~~\mathop {,} _{}\\&{\text{v}}\_{\text{1}}=0.0000{\text{466}}~~~\mathop {,} _{}{\text{v}}\_{\text{2}}=0.0000{\text{4438}}\\\end{aligned}}$

استوانه بلند افقی

درباره استوانه‌های بلند افقی خیلی مطالعه شده است وبسیاری از رابطه‌های موجود توسط مورگان ارائه شده است. این رابطه برای یک استوانه با دمای ثابت چنین است:

${\bar {N}}{{u}_{D}}={\frac {{\bar {h}}D}{k}}=CRa_{D}^{n}$

ثابت‌های $C,n$ در جدول زیر آورده شده‌اند.

${\begin{matrix}R{{a}_{D}}&C&n\\{{10}^{-10}}-{{10}^{-2}}&0.675&0.058\\{{10}^{-2}}-{{10}^{2}}&1.02&0.148\\{{10}^{2}}-{{10}^{4}}&0.850&0.188\\{{10}^{4}}-{{10}^{7}}&0.480&0.250\\{{10}^{7}}-{{10}^{12}}&0.125&0.333\\\end{matrix}}$

چرچیل و چو رابطه‌ای را برای گستره وسیعی از عدد ریلی داده‌اند:

${\overline {\mathrm {Nu} }}_{L}\ ={\left[0.6+{\frac {0.387\mathrm {Ra} _{D}^{1/6}}{\left[1+(0.559/\mathrm {Pr} )^{9/16}\,\right]^{8/27}\,}}\right]}^{2}\quad \mathrm {Ra} _{L}\leq 10^{12}$

رابطه بالا عدد نوسلت متوسط در تمام محیط استوانه تک دما را می‌دهند.

مثال) در شکل مقابل برای خنک کردن تراشه‌های الکترونیکی جریان هوا با دمای ${{T}_{in}}={{85}^{\circ }}F$ و دبی $22{\frac {f{{t}^{3}}}{\min }}$ از آن عبور می‌دهیم و دمای هوای خروجی برابر است با ${{T}_{out}}={{100}^{\circ }}F$

دمای سطح لوله را بیابید. از مقاومت حرارتی لوله صرف نظر شود.

توضیحات:
۱-گرمایی که توسط تراشه‌های الکترونیکی تولید می‌شود قسمتی توسط جابجایی اجباری و قسمتی دیگر توسط جابجایی آزاد دفع می‌شود. به عبارتی $q={{q}_{F.c}}+{{q}_{N.c}}$
۲-برای محاسبه ${{q}_{F.c}}$ چونکه دمای ورود و خروج معلومند می‌توانیم با استفاده از فرمول ${{q}_{F.c}}={\dot {m}}{{c}_{p}}({{T}_{out}}-{{T}_{in}})$ آن را بدست می‌آوریم، که در آن ${{c}_{p}}$ را در متوسط دمای ورود و خروج می‌خوانیم.
۳-برای بدست آوردن ${{T}_{s}}$ چونکه ${\overline {h}}$ نامعلوم است، از روش حدس و خطا استفاده می‌کنیم. ابتدا ${{T}_{s}}$ را حدس زده و سپس با استفاده از جابجایی آزاد ${\overline {h}}$ را بدست می‌آوریم و سپس با استفاده از فرمول (*) که در زیر آمده است، ${{T}_{s}}$ جدید را بدست می‌آوریم اگر با ${{T}_{s}}$ حدس زده شده اختلاف کمی داشت جواب است در غیر اینصورت دوباره محاسبات را بر مبنای ${{T}_{s}}$ جدید حل می‌کنیم.

${\begin{aligned}&q={{q}_{F.c}}+{{q}_{N.c}}\\&{{q}_{F.c}}={\dot {m}}{{c}_{p}}\left({{T}_{out}}-{{T}_{in}}\right)\\&{{q}_{N.c}}=h{{A}_{s}}\left({{T}_{s}}-{{T}_{\infty }}\right)\Rightarrow {{T}_{s}}={{T}_{\infty }}+{\frac {q-{{q}_{F.c}}}{h{{A}_{s}}}}\left(*\right)\\&{\dot {m}}=1.58\left[{\frac {lbm}{\min }}\right]\\&T={{T}_{in}}\to \rho =0.072{\frac {lbm}{f{{t}^{3}}}}\\&T={\frac {{{T}_{out}}+{{T}_{in}}}{2}}\to {{c}_{p}}=0.24{\frac {Btu}{lb{{m}^{\circ }}F}}\\&\Rightarrow {{q}_{F.c}}=342{\frac {btu}{hr}}\\&\Rightarrow {{q}_{N.c}}=272{\frac {btu}{hr}}\\\end{aligned}}$

برای حل مسئله باید از روش سعی و خطا استفاده کنیم:
حدس اولیه: ${{T}_{s}}={{150}^{\circ }}F$

${\begin{aligned}&{{T}_{f}}={\frac {{{T}_{s}}+{{T}_{\infty }}}{2}}={{115}^{\circ }}F\to \left\{{\begin{aligned}&k=0.0156\\&\Pr =0.73\\&\beta ={\frac {1}{{T}_{f}}}={\frac {1}{115+490}}=0.0017{{R}^{-1}}\\&\nu =0.189*{{10}^{-3}}{\frac {f{{t}^{2}}}{s}}\\\end{aligned}}\right.\\&R{{a}_{D}}={\frac {g\beta ({{T}_{s}}-{{T}_{\infty }}){{D}^{3}}}{{\nu }^{2}}}\Pr =2.93*{{10}^{6}}\\&{{\overline {Nu}}_{D}}={{\left\{0.6+{\frac {0.387R{{a}_{D}}^{\frac {1}{6}}}{{\left[1+{{\left({\frac {0.559}{\Pr }}\right)}^{\frac {9}{16}}}\right]}^{\frac {8}{27}}}}\right\}}^{2}}=19.8\\&\to {\overline {h}}={\frac {K}{D}}{\overline {N{{u}_{D}}}}=0.926\\&{{A}_{s}}=\pi DL=4.19f{{t}^{2}}\\&\left(*\right)\Rightarrow {{T}_{s}}={{149.9}^{\circ }}F\\\end{aligned}}$

چونکه اختلاف دمای بین حدس اولیه و جواب بدست آمده کم است، پس حل مسئله به همین جا ختم می‌شود ولی اگر اختلاف زیاد بود دمایی که بدست آورده بودیم را به عنوان حدس جدید می‌گرفتیم و مسئله را دوباره حل می‌کردیم تا اینکه اختلاف دماها کم شود.

حال فرض کنید در مسئله بالا دمای خروجی نیز مجهول باشد. در این صورت معادلات حاکم که از طریق موازنه انرژی بدست آمده‌اند به صورت زیر در خواهد آمد:

${\begin{aligned}&{{q}_{el}}={{q}_{N.C.}}+{{q}_{F.C.}}\\&{{q}_{N.C.}}={{h}_{out}}.A.({{T}_{s}}-{{T}_{\infty }})\\&{{q}_{F.C.}}={\dot {m}}.{{C}_{P}}.({{T}_{out}}-{{T}_{in}})\\&{{q}_{F.C.}}={{h}_{in}}.A.\Delta {{T}_{log}}\\&\Delta {{T}_{log}}={\frac {({{T}_{out}}-{{T}_{s}})-({{T}_{in}}-{{T}_{s}})}{ln({\frac {{{T}_{out}}-{{T}_{s}}}{{{T}_{in}}-{{T}_{s}}}})}}\\\end{aligned}}$

که در آن ${{\operatorname {h} }_{in}}$ که مربوط به جابه جایی اجباری داخل لوله است از روابط زیر بدست می‌آید:

${\begin{aligned}&{{\operatorname {h} }_{in}}=N{{u}_{in}}k/D\\&{{\operatorname {Nu} }_{in}}=0.023.{{(Re)}^{({\frac {4}{5}})}}.P{{r}^{0.3}}\\&\operatorname {Re} ={\frac {U.3600[s/hr].D}{\nu }}\\\end{aligned}}$

در رابطه بالا خواص در دمای متوسط ورودی و خروجی لوله خوانده می‌شود. همچنین ${{\operatorname {h} }_{out}}$ را از روابط زیر بدست می‌آوریم:

${\begin{aligned}&{{h}_{out}}=N{{u}_{out}}k/D\\&N{{u}_{out}}={{(0.6+{\frac {0.387*R{{a}^{(1/6)}}}{{(1+{{({\frac {0.559}{Pr}})}^{\frac {9}{16}}})}^{\frac {8}{27}}}})}^{2}}\\&Ra={\frac {g.\beta .({{T}_{s}}-{{T}_{\infty }}).{{D}^{3}}.12960000[{{s}^{2}}/h{{r}^{2}}]}{{\nu }^{2}}}\\\end{aligned}}$

که در معادلات مربوط به جابه جایی آزاد خارجی خواص در ${{\operatorname {T} }_{film}}={\frac {{{T}_{s}}+{{T}_{\infty }}}{2}}$ خوانده می‌شوند.

همانطور که مشاهده می‌کنید دمای سطح و دمای خروجی در معادلات بالا مجهول بوده و باید مسئله با روش سعی و خطا حل شود.

با نوشتن این معادلات و حل آنها در نرم‌افزار EES این نتایج بدست آمده است:

${\begin{aligned}&{{T}_{s}}=80.81{}^{{}^{\circ }}F\\&{{T}_{out}}=85.44{}^{{}^{\circ }}F\\\end{aligned}}$

کره

چرچیل رابطه زیر را برای کره‌ها در سیالات با شروط $\Pr \rangle 0.7$ & شکست در تجزیه (پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین (توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی) ("Math extension cannot connect to Restbase.") از سرور "http://localhost:6011/fa.wikibooks.org/v1/":): {\displaystyle Ra\rangle {{10}^{۱۱}}} را داده است:

${\overline {\mathrm {Nu} }}_{D}\ =2+{\frac {0.589\mathrm {Ra} _{D}^{1/4}}{\left[1+(0.469/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}$

در حد وقتی $R{{a}_{D}}\to 0$ معادله بالا به صورت ${\bar {N}}{{u}_{D}}=2$ در می‌آید. این عدد ناسلت متناطر است با انتقال گرمای رسانشی بین یک سطح کروی و محیط وسیع و ساکنی که این کره در آن قرار دارد.

حال برای درک بیشتر مفاهیم یک مثال حل شده ارائه می‌کنیم.

مثال) لوله افقی، حامل بخار آب در فشار زیاد، با قطر خارجی ۰٫۱ متر از اتاق بزرگی که دمای دیوارها و هوای داخل آن ۲۳ درجه سانتیگراد است عبور می‌کند. دمای سطح خارجی لوله ۱۶۵ درجه سانتیگراد و گسیلمندی آن ۰٫۸۵ است. دفع گرما از طول واحد لوله را تخمین بزنید.

فرضیات

مساحت سطح لوله در مقایسه با اطراف کوچک است.
جابجایی آزاد داریم

ابتدا دمای فیلم را محاسبه می‌کنیم

$T_{f}={\frac {296+438}{2}}=367K$

حال خواص هوا را از جدول الف -۴ کتاب انتقال حرارت اینکروپرا می‌خوانیم

$\nu =22.8\times {{10}^{-6}}$

$\alpha =32.8\times {{10}^{-6}}$

$\Pr =0.697$

$\beta =2.725\times {{10}^{-3}}$

\mathrm {Ra} _{D}=\mathrm {Gr} _{D}\mathrm {Pr} ={\frac {9.8(2.725*10^{-3})}{(22.8*10^{-6})(32.8*10^{-6})}}(165-23)0.1^{3}=5.073*10^{6}

حال باید ناسلت متوسط را به دست‌آورد:

${\overline {\mathrm {Nu} }}_{D}\ ={\left[0.6+{\frac {0.387\mathrm {Ra} _{D}^{1/6}}{\left[1+(0.559/\mathrm {Pr} )^{9/16}\,\right]^{8/27}\,}}\right]}^{2}={\left[0.6+{\frac {0.387\mathrm {(} 5.073*10^{6})^{1/6}}{\left[1+(0.559/\mathrm {0.697} )^{9/16}\,\right]^{8/27}\,}}\right]}^{2}=23.3\quad \mathrm {Ra} _{D}\leq 10^{12}$

${\overline {\mathrm {h} }}={\frac {{\overline {\mathrm {Nu} }}_{D}k}{D}}=0.0313(23.3)/0.1=7.29$

$q={{q}_{conv}}+{{q}_{rad}}=7.29\pi (0.1)(165-23)+0.85\pi (5.67)\times {{10}^{-8}}({{438}^{4}}-{{296}^{4}})=325+441=766$

جابجایی آزاد در کانال‌های متشکل از صفحات موازی

الف: جابجایی آزاد درون کانال قائم

توجه شود که این فرض و روابط مربوط به آن؛ زمانی صادق است که فاصله صفحه‌ها از هم خیلی زیاد نباشد. در حالت دما ثابت:

${\begin{array}{*{35}{l}}{}&{\bar {N}}{{u}_{s}}=({\frac {\frac {q}{A}}{{{T}_{s}}-{{T}_{\infty }}}}){\frac {S}{k}}\\{}&{}\\\end{array}}{\overline {N{{u}_{s}}}}={\frac {1}{24}}R{{a}_{s}}\left({\frac {S}{L}}\right){{\left\{1-\exp \left({\frac {-35}{R{{a}_{s}}\times {\frac {S}{L}}}}\right)\right\}}^{\frac {3}{4}}}$

شرط استفاده از معادله بالا:

${\text{(}}{{10}^{-1}}<{\frac {S}{L}}\times R{{a}_{s}}<{{10}^{5}})$

در این رابطه عدد ناسلت متوسط و عدد رایلی به ترتیب عبارتند از :

${\bar {N}}{{u}_{s}}=({\frac {\frac {q}{A}}{{{T}_{s}}-{{T}_{\infty }}}}){\frac {S}{k}}$

$R{{a}_{s}}={\frac {g\beta ({{T}_{s}}-{{T}_{\infty }}){{S}^{3}}}{\alpha \nu }}$

وقتی s نسبت به L خیلی کوچک باشد؛ لایه‌های مرزی خیلی زود به هم می‌رسند: در شرا یط توسعه یافته که داشته باشیم:

${\frac {S}{L}}\ll 1$

خواهیم داشت

${\overline {N{{u}_{s}}}}={\frac {1}{24}}\times R{{a}_{s}}\left({\frac {S}{L}}\right)$

در حالت شار ثابت:

${\overline {N{{u}_{s}}}}=0.144{{\left[R{{a}_{s}}^{*}\left({\frac {S}{L}}\right)\right]}^{0.5}}$

که:

$R{{a}_{s}}^{*}={\frac {g\beta q''{{s}^{4}}}{k\alpha \nu }}$

برای کانال تک شار نامتقارن با یک سطح عایق:

${\bar {N}}{{u}_{s,L(fd)}}=0.204{{(Ra_{s}^{*}({\frac {S}{L}}))}^{{}^{1}\!\!\diagup \!\!{}_{2}\;}}$

رابطه بار - کوهن - روسنو :

برای حالت دما ثابت:

${\overline {N{{u}_{s}}}}={{\left[{\frac {{C}_{1}}{{\left(R{{a}_{s}}\left({\frac {S}{L}}\right)\right)}^{2}}}+{\frac {{C}_{2}}{{\left(R{{a}_{s}}\left({\frac {S}{L}}\right)\right)}^{0.5}}}\right]}^{-0.5}}$

و برای حالت شار ثابت:

${\overline {N{{u}_{s}}}}={{\left[{\frac {{C}_{1}}{\left(R{{a}_{s}}^{*}\left({\frac {S}{L}}\right)\right)}}+{\frac {{C}_{2}}{{\left(R{{a}_{s}}^{*}\left({\frac {S}{L}}\right)\right)}^{\frac {2}{5}}}}\right]}^{-0.5}}$

مقادیر ${{C}_{1}}{\text{ , }}{{\text{C}}_{2}}$ از جدول ۹-۳ کتاب اینکروپرا صفحه ۵۳۴ خوانده می‌شوند.

در حالت حدی وقتی S خیلی زیاد شود:

${\frac {\overline {{h}_{s}}}{k}}={\frac {1}{24}}\times \left(R{{a}_{s}}\left({\frac {S}{L}}\right)\right){{\left({\frac {35}{R{{a}_{s}}\left({\frac {S}{L}}\right)}}\right)}^{\frac {3}{4}}}$

$\to {\frac {\overline {{h}_{s}}}{k}}\times {\frac {L}{S}}=0.6{{\left(R{{a}_{s}}\times {{\left({\frac {L}{S}}\right)}^{3}}\right)}^{0.25}}\to {\overline {N{{u}_{L}}}}=0.6R{{a}_{L}}^{0.25}$

در حالتی که مطابق شکل؛ صفحه‌ای به عرضW داشته باشیم وبخواهیم تعداد بهینه تیغه‌ها برای بالاترین نرخ انتقال حرارت از صفحه را بیابیم؛ باید به دو نکته توجه کنیم:اولا هر چه فاصله تیغه‌ها کمتر باشد؛ تعداد بیشتری تیغه در این فاصله قرار می‌گیرد ثانیا هر چه فاصله دو تیغه به هم نزدیکتر باشد؛ لایه‌های مرزی زودتر به هم رسیده و تنش برشی ایجاد شده باعث ایجاد مقاومت در برابر جریان شده و h کم شده و در نتیجه انتقال حرارت کاهش می‌یابد. پس باید به دنبال تعداد بهینه صفحات باشیم. برای این منظور، فاصله بهینه بین دو صفحه مجاور را می‌یابیم.

فرض می‌کنیم: ${{T}_{{S}_{1}}}={{T}_{{S}_{2}}}$ در نتیجه:

${{S}_{opt}}={\frac {2.71}{\left({\frac {R{{a}_{s}}}{L{{S}^{3}}}}\right)}}\times {\frac {L}{L}}={\frac {2.71\times L}{R{{a}_{L}}^{0.25}}}$

وتعداد بهینه تیغه‌ها برابر خواهد بود با:

$n={\frac {w}{{{S}_{opt}}+t}}$

پس در نهایت روش حل مساله بصورت زیر است:

${\overline {{h}_{s}}}={\frac {{\overline {N{{u}_{s}}}}\times k}{{S}_{opt}}}\to q=n{\overline {{h}_{s}}}{{A}_{S}}\left({{T}_{S}}-{{T}_{\infty }}\right)$

ب: جابجایی آزاد درون کانال‌های مایل و افقی

جابجایی آزاد در جریان‌های داخلی

محفظه

برای سیال ساکن

$q=kA{\frac {{{T}_{H}}-{{T}_{C}}}{L}}$

${{k}_{eff}}={\overline {N{{u}_{L}}}}\times k$

برای جابجایی آزاد

$q=hA\left({{T}_{H}}-{{T}_{C}}\right)={\overline {N{{u}_{L}}}}{\frac {kA\left({{T}_{H}}-{{T}_{C}}\right)}{L}}={{k}_{eff}}{\frac {A\left({{T}_{H}}-{{T}_{C}}\right)}{L}}$

حل مسئله با نرم‌افزار :

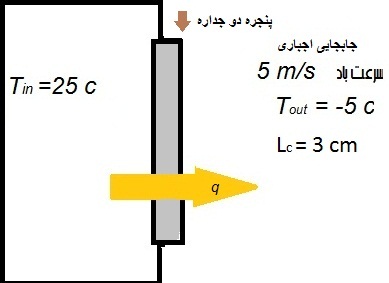
مطلوب است مقدار شار انتقال گرما عبوری از شیشه دو جداره به ابعاد ۱٫۲ ×۲.(داده‌های دیگر مسئله رادر شکل می‌بینید)

در این مثال باید یکی از مقاومت‌ها و اختلاف دمای دو سر ان مقاومت گرمایی را داشته باشیم تا بتوانیم شار انتقال گرما را بیابیم. دراین مسئله سه مقاومت شامل مقاومت جابجایی ازاد داخل اتاق و جابجایی ازاد محفظه (فضای بین شیشه دوجداره) وجابجایی اجباری هوای بیرون وجود دارد. برای محاسبهٔ مقاومت گرمایی هریک نیاز به داشتن نوسلت وبرای یافتن نوسلت نیاز به دانستن مقدار خواص و برای خواص نیز نیاز به داشتن دمای سطح داریم که در سوال داده نشده پس نیاز به یک روند سعی و خطا داریم. این مسئله با نرم‌افزار EES حل شده و جواب‌های مسئله به ترتیب ضریب جابجایی هوای داخل اتاق، دمای سطح داخلی پنجره، ضریب جابجایی اجباری هوای بیرون، دمای سطح بیرونی پنجره، ضریب جابجایی هوای بین شیشه‌های پنجره دو جداره و نرخ انتقال حرارت به صورت زیر در امده است.

${\begin{aligned}&{\overline {{h}_{in}}}=1.598({w}/{m.k)}\;\\&{{T}_{s,in}}=296.3(k)\\&{\overline {{h}_{out}}}=7.681({w}/{m.k)}\;\\&{{T}_{s,out}}=268.5(k)\\&{\overline {{h}_{middle}}}=0.605({w}/{m.k)}\;\\&q=7.011(w)\\\end{aligned}}$

برای توضیح بیشتردر مورد روند سعی وخطا اینکه ابتدا دمای سطح داخلی (Ts_in)را حدس می‌زنیم وسپس با محاسبهٔ دمای فیلم خواص هوا را می‌خوانیم چون با داشتن خواص مقاومت‌های تشعشعی و جابجایی ازاد دخل اتاق بدست می ایند(R_radو R_in conv) پس انتقال گرما قابل محاسبه است. حال برای جابجایی ازاد داخل شیشه دو جداره سعی وخطا می‌کنیم وباید خواص هوای داخل شیشه دو جداره را در دمای سطح داخلی بخوانیم وسپس مقاومت هوای داخل را محاسبه کرد(R_mid conv) حال می‌توانیم با داشتن نرخ انتقال گرما واندازهٔ مقاومت دمای سطح بیرونی را بدست اورد(T_s out)وازان دمای فیلم بیرون رابدست اورد وسپس با خواندن خواص از جدول مقاومت بیرونی(R_out conv) را محاسبه کرد حال باید نرخ انتقال گرمایی خروجی از سطح بیرونی را بدست اورد و با گذاشتن در معادله گرمایی اولی که برای داخل اتاق نوشتیم مقدار دمای سطح داخلی جدید شیشه دو جداره را بدست اورد همانطور که می‌بینیم سیکل کامل است چون در ابتدا دمای سطح داخلی یعنی Ts_in را حدس زدیم ودراخر هم به خودش رسیدیم.

نمودار مقاومت گرمایی حاکم بر مسئله مطابق شکل است.

استوانه‌های هم مرکز

در زیر انتقال گرمای جا به جایی آزاد را در فضای حلقوی بین استوانه‌های افقی هم مرکز بلند بررسی کرده‌ایم. اگر استوانه داخلی گرم و استوانه خارجی سرد باشد (Ti>To)، سیال در امتداد استوانه‌های داخلی و خارجی، به ترتیب، بالا و پایین می‌رود. اگر Ti<To، جریان معکوس می‌شوند. آهنگ انتقال گرما در طول واحد استوانه (W/m) را به صورت زیر می تون بیان کرد:

{q}'={\frac {2\pi {{k}_{eff}}}{\ln({}^{{D}_{o}}\!\!\diagup \!\!{}_{{D}_{i}}\;)}}({{T}_{i}}-{{T}_{o}})

که در آن رسانندگی گرمایی موثر Keff عبارت است از رسانندگی گرمایی که سیال ساکنی باید دارا باشد تا همان مقدار گرمایی را انتقال دهد که سیال متحرک می‌دهد. رابطه زیر برای Keff پیشنهاد شده است.

(1)

{\frac {{k}_{eff}}{k}}=0.386{{({\frac {{p}_{r}}{0.861+{{p}_{r}}}})}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}{{(Ra_{c}^{*})}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}

که در آن

Ra_{c}^{*}={\frac {{\left[\ln \left({}^{{D}_{o}}\!\!\diagup \!\!{}_{{D}_{i}}\;\right)\right]}^{4}}{{{L}^{3}}{{\left(D_{i}^{-{\frac {3}{5}}}+D_{o}^{-{\frac {3}{5}}}\right)}^{5}}}}R{{a}_{L}}

از معادله (۱) در گستره۱۰۰۰۰۰۰۰> $Ra_{c}^{*}$ >100 و $0.7\leq \Pr \leq 6000$ می‌توان استفاده کرد. برای 100>Ra، Keff=k. کیون و گلدشتین رابطه‌ای تفصیلی تر داده‌اند که اثر خروج از مرکز استوانه را در نظر می‌گیرد.

کره‌های هم مرکز

انتقال گرمای جابه جایی آزاد بین کره‌های هم مرکز را نیز بررسی و رابطهٔ زیر را برای آهنگ انتقال گرما داده‌ایم.

q={{k}_{eff}}\pi \left({\frac {{{D}_{i}}{{D}_{o}}}{L}}\right)\left({{T}_{i}}-{{T}_{o}}\right)

رسانندگی گرمایی موثر عبارت است از

{\frac {{k}_{eff}}{k}}=0.74{{({\frac {{p}_{r}}{0.861+{{p}_{r}}}})}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}{{(Ra_{s}^{*})}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}

که در آن

Ra_{s}^{*}=\left[{\frac {L}{{\left({{D}_{o}}{{D}_{i}}\right)}^{4}}}{\frac {R{{a}_{L}}}{{\left(D_{i}^{-{\frac {7}{5}}}+D_{o}^{-{\frac {7}{5}}}\right)}^{5}}}\right]

از این رابطه در گستره ۱۰۰۰۰> $Ra_{s}^{*}$ >۱۰۰ و شکست در تجزیه (خطای نحوی): {\displaystyle ۰٫۷\le \Pr \le ۴۰۰۰}

با تقریب خوب می‌توان استفاده کرد.

مثال) شیشیه دو جداره‌ای داریم که محفظهبین دو شیشه پر از هوای اتمسفریک است. ابعاد آن بدین صورت است که ضخامت آنL=.6m وارتفاع آن h=1.2m و طول آن w=0.8m می‌باشد و دماهای دو طرف آن به ترتیب ۱۰ - و ۲۰ درجه سانتی گراد می‌باشد. مقدار q را بدست آورید.

${{T}_{f}}={\frac {{{T}_{1}}+{{T}_{2}}}{2}}=5{}^{\circ }c\Rightarrow$

با استفاده از جدول خواص

$\upsilon =13.9\times {{10}^{-6}}{}^{{m}^{2}}\!\!\diagup \!\!{}_{s}\;,k=0.0245{}^{w}\!\!\diagup \!\!{}_{m\cdot k}\;$

$\alpha =19.6\times {{10}^{-6}}{}^{{m}^{2}}\!\!\diagup \!\!{}_{s}\;,\Pr =.71,\beta =0.0036{{k}^{-1}}$

$R{{a}_{L}}={\frac {q\beta \left({{T}_{1}}-{{T}_{2}}\right){{L}^{2}}}{\upsilon \alpha }}=8.37\times {{10}^{5}}$

${}^{H}\!\!\diagup \!\!{}_{L}\;=20$

${\overline {N{{u}_{L}}}}=0.42R{{a}_{L}}^{.25}{{\Pr }^{0.012}}{{\left({}^{H}\!\!\diagup \!\!{}_{L}\;\right)}^{-0.3}}$

${\overline {h}}={\overline {N{{u}_{L}}}}{\frac {k}{L}}=2.1{}^{w}\!\!\diagup \!\!{}_{{{m}^{2}}\cdot k}\;$

$q={\overline {h}}A\left({{T}_{1}}-{{T}_{2}}\right)={\overline {h}}wH\left({{T}_{1}}-{{T}_{2}}\right)=61w$

مثال ۲) یک سیم عایق مفروض است. اگر هوای ساکن با T=۳۰ درجه سانتی گراد داشته باشیم دمای سطح سیم و دمای ماکزیمم (روی جداره داخلی عایق) را بیابید.

${\begin{aligned}&D_{i}=3mm\\&D_{o}=6mm\\&T_{\infty }=30^{0}C\\&L=12mm\\&{\dot {Q}}=80w\\&\varepsilon =0.9\\&T_{MAX}\\&\\&q=q_{conv}+q_{rad}={\bar {h}}A(T_{S}-T_{\infty })+\varepsilon \sigma A(T_{S}^{4}-T_{\infty }^{4})\\&\\&if\to T_{s}=50\to T_{f}=40^{0}C\to \left\{{\begin{aligned}&K=0.0466{\frac {w}{mk}}\\&v=1.7*10^{-5}{\frac {m^{2}}{s}}\\&\Pr =0.72\\&\beta ={\frac {1}{T_{f}}}=0.0032k^{-1}\\\end{aligned}}\right\}\\&\to Ra_{D}={\frac {g\beta (T_{s}-T_{\infty })D^{3}\Pr }{v^{2}}}=339.3\\&{\bar {N}}u_{D}=(0.6+{\frac {0.387Ra_{D}^{\frac {1}{6}}}{(1+(0.559/\Pr )^{9/16})^{8/27}}})^{2}=2.1\\&\\&\to {\bar {h}}=9.33{\frac {w}{m^{2}k}}\\&\\&A=\pi D_{2}L,{\bar {h}}\to T_{S}=52.6^{0}C\\&\\&R_{th}={\frac {\ln({\frac {D_{2}}{D_{1}}})}{2\pi KL}}\\&\\&T_{MAX}-T_{S}=qR_{th}\to T_{MAX}=57.5^{0}C\\&\\\end{aligned}}$ ................................................................................ مثال:

اگر در لوله‌ای به قطر 2cm و ${\overset {\centerdot }{\mathop {\forall } }}\,=8{\frac {lit}{\min }}$ و ${{T}_{i}}=10{\overset {{}^{\circ }}{\mathop {C} }}\,$ و ${{T}_{0}}=80{\overset {{}^{\circ }}{\mathop {C} }}\,$ و $L=7m$ باشد مقادیر ${{T}_{s,l}}$ و $q$ را بیابید. (لوله حاوی آب می‌باشد و شار ثابت است)

حل:

$q={\overset {\centerdot }{\mathop {m} }}\,{{C}_{p}}({{T}_{0}}-{{T}_{i}})$

خواص آب در دمای ${\overline {T}}$ :

${\overline {T}}={\frac {1}{2}}({{T}_{i}}+{{T}_{0}})=318K$

از جدول:

${\begin{aligned}&\rho =990{\frac {kg}{{m}^{3}}}\\&K=0.637{\frac {w}{mk}}\\&\upsilon =0.602\times {{10}^{-6}}{\frac {{m}^{2}}{s}}\\&\Pr =3.91\\&{{C}_{p}}=4180{\frac {j}{kg}}\\&{\overset {\centerdot }{\mathop {v} }}\,={\frac {8\times {{10}^{-3}}}{60}}{\frac {{m}^{3}}{s}}\\\end{aligned}}$

داریم:

${\begin{aligned}&{\overset {\centerdot }{\mathop {m} }}\,=\rho {\overset {\centerdot }{\mathop {v} }}\,\to {\overset {\centerdot }{\mathop {m} }}\,=0.132{\frac {kg}{s}}\\&q={\overset {\centerdot }{\mathop {m} }}\,{{C}_{p}}({{T}_{0}}-{{T}_{i}})\to q=38623\left[w\right]\\&{{V}_{m}}={\frac {{\overset {\centerdot }{\mathop {\forall } }}\,}{{A}_{c}}}={\frac {1.33\times {{10}^{-4}}}{\pi {{(2\times {{10}^{-2}})}^{2}}}}=0.2122{\frac {m}{s}}\\&\operatorname {Re} =14100\\&N{{u}_{D}}=82.8\to h=2637{\frac {w}{{{m}^{2}}k}}\\&{q}''={\frac {q}{{A}_{s}}}=h({{T}_{s,l}}-{{T}_{0}})\to {{T}_{s,l}}=113.3{\overset {{}^{\circ }}{\mathop {C} }}\,\\\end{aligned}}$

توجه: سوال بالا مربوط به قسمت جابجایی اجباری درون لوله است و جای آن در این قسمت نیست. اما برای مقایسه این دو حالت و پرهیز از اشتباه بدنیست.

همانطور که می‌بینید جریان مغشوش است و برای محاسبه Nu در دمای میانگین ورودی و خروجی از رابطه زیر استفاده شده است:

                                                        $N{{u}_{D}}={\frac {hD}{k}}=.023{{\operatorname {Re} }^{0.8}}{{\Pr }^{0.4}}$

باید توجه داشت که اگر در اطراف لوله جابجایی آزاد داشته باشیم برای خواندن خواص و محاسبه Nu اولا هرگز نباید از میانگین دمای ورودی و خروجی استفاده کرد، بلکه در دمای میانگین سطح و هوای ساکن می‌خوانیم. ثانیا باید خواص هوا را بخوانیم نه سیال درون لوله. برای روشن شدن مطلب در سوال بالا فرض می‌کنیم که روی سطح جابجایی آزاد با هوا در دمای ${{T}_{\infty }}={{20}^{{}^{\circ }}}c$ وجود دارد و شرایط پایا باشد، دراین صورت باید یک ${{T}_{s}}$ حدس بزنیم به صورت زیر:

حدس ${{T}_{s}}={{35}^{{}^{\circ }}}c$

${{T}_{f}}={\frac {{{T}_{s}}+{{T}_{\infty }}}{2}}={{300.5}^{{}^{\circ }}}k$

خواص هوا در   ${{T}_{f}}=300.5$

${\begin{aligned}&\upsilon =15.89\times {{10}^{-6}}{\frac {{m}^{2}}{s}},k=26.3\times {{10}^{-3}}{\frac {w}{m{}^{{}^{\circ }}k}},\Pr =.707,\beta ={\frac {1}{{T}_{f}}}=.0033{\frac {1}{{}^{{}^{\circ }}k}}\\&Ra={\frac {g\beta ({{T}_{s}}-{{T}_{\infty }}){{D}^{3}}}{{\upsilon }^{2}}}\Pr =10.86\times {{10}^{7}}\\\end{aligned}}$

برای جابجایی آزاد حول استوانه باید با استفاده از خواص هوا مقدار Nu را از رابطه زیر بدست آوریم:

${\begin{aligned}&N{{u}_{D}}={{\left[.6+{\frac {.387R{{a}^{\frac {1}{6}}}}{{\left[1+{{({\frac {.559}{\Pr }})}^{\frac {9}{16}}}\right]}^{\frac {8}{27}}}}\right]}^{2}}=58\\&{{h}_{\text{out}}}={\frac {k.Nu}{D}}=76.27\\\end{aligned}}$

چون شرایط پایا است مقدار گرمایی که مایع به سطح لوله می‌دهد با گرمایی که سطح لوله از طریق جابجایی در مجاورت هوا از دست می‌دهد برابر است.

${\begin{aligned}&{{q}_{in}}={{q}_{out}}\to q={{h}_{out}}\times A({{T}_{s}}-{{T}_{\infty }})=38623\\&{{T}_{s}}=1170{}^{{}^{\circ }}c\\\end{aligned}}$

البته این دما خیلی زیاد است. در حقیقت در اینجا ما از گرمایی که خود سیال در ورودی به حجم کنترل وارد می‌کند در صورت سوال صرفنظر کردیم و دما زیاد بدست آمد.

ویکی‌جزوه/دانشکده:فنی و مهندسی/انتقال حرارت/جابجایی آزاد

فهرست